Scala Coroutines

First-Class Type-Safe Coroutines in Scala

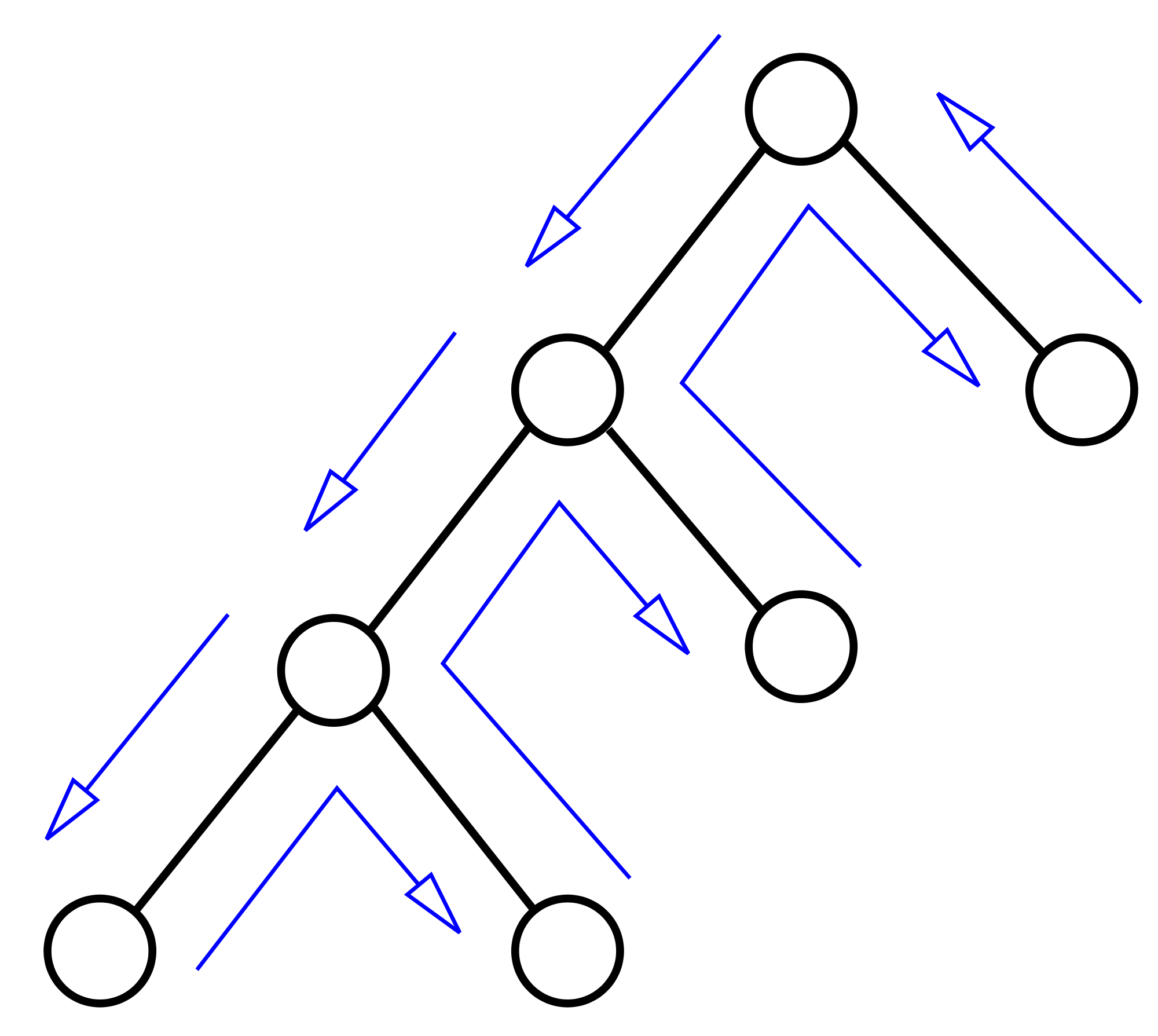
Behavior trees

A planning model in which an AI agent decides on the next action by traversing a special data structure called a behavior tree.

Every behavior tree is composed of two node types:
task nodes and control nodes.

Task nodes

They are the leaf nodes of a behavior tree.

They execute a side-effect, and return running, success or failure status.

Task nodes

They are the leaf nodes of a behavior tree.

They execute a side-effect, and return running, success or failure status.

Task nodes

They are the leaf nodes of a behavior tree.

They execute a side-effect, and return running, success or failure status.

Control nodes

Control nodes are inner nodes that bind subtrees together.

Given a set of subtrees and their return values, a control node decides whether to run some subtree, or return a success or failure status.

Two basic control nodes: sequence and selector.

Behavior trees can compose

The main reason behind their popularity.

Different subtrees can be developed, tuned and tested independently, and then merged into larger functional units.

Behavior tree extensions

The basic model can be extended with nodes such as
repeaters, randomizers or inverters.

Behavior tree DSLs

<?xml version="1.0" encoding="UTF-8"?>
<agent>
  <selector>
    <sequence name="capture-the-flag>
      <task name="move"></task>
      <task name="take-the-flag"></task>
    </sequence>
    <module name="defend-the-base">
    </module>
  </selector>
</agent>

Remind you of another tree you know?

Isomorphism

Behavior tree planner is nothing more than an AST interpreter.

Behavior tree downsides

AI researchers have been rediscovering the wheel.

implementing behavior trees is unintuitive
nobody likes XML
essentially an AST interpreter - bad performance
harder to debug

Why not just use a programming language?


def agent() = {
  captureTheFlag() || defendTheBase()
}

def captureTheFlag(): Boolean = {
  move() && takeTheFlag()
}

Why not just use a programming language?


def agent() = {
  captureTheFlag() || defendTheBase()
}

def captureTheFlag(): Boolean = {
  move() && takeTheFlag()
}

Most languages cannot suspend computation and resume it later.

Coroutines - the missing link

A programming construct that allows suspending the computation (i.e. yielding), and resuming it later from the point where it was suspended.


def captureTheFlag(): Boolean = {
  yield(move()) && takeTheFlag()
}

Goals of this talk

Demonstrate how coroutines work in Scala
Show how Scala coroutines generalize other approaches

Subroutines


val double = (x: Int) => x + x


double(7)

Calling a subroutine

val double = (x: Int) => x + x
double(7)

Calling a subroutine

val double = (x: Int) => 7 + 7
double(7)

Calling a subroutine

val double = (x: Int) => 14
double(7)

Calling a subroutine

val double = ...
14

Calling a subroutine

A function invocation is an entity that exists during program execution.

However, the callsite cannot observe the existence of that entity.

Coroutine definition


val double =
  (x: Int) => x + x

Coroutine definition


val double = coroutine {
  (x: Int) => x + x
}

This coroutine does not yield.

The yieldval construct suspends computation
and yields a value to the caller.

Coroutine definition


val double = coroutine { (x: Int) =>
  yieldval(x)
  yieldval(x)
}

Calling a coroutine

Coroutine invocation is resumed by the caller.
Therefore, it is an observable entity in the program.

Calling a coroutine


val double = coroutine { (x: Int) =>
  yieldval(x)
  yieldval(x)
}

val i = call(double(7))

A coroutine invocation can be observed by the callsite.

Therefore, it must be a first-class object.

Calling a coroutine


val double = coroutine { (x: Int) =>
  yieldval(x)
  yieldval(x)
}

val i = call(double(7))

var sum = 0

while (i.resume) { sum += i.value }

Calling a coroutine


val double = coroutine { (x: Int) =>
 ↑yieldval(x)
  yieldval(x)
}

val i = call(double(7))↑
var sum = 0
while (i.resume) { sum += i.value }

Calling a coroutine


val double = coroutine { (x: Int) =>
 ↑yieldval(x)
  yieldval(x)
}

val i = call(double(7))
var sum = 0
while (i.resume↑) { sum += i.value }

Calling a coroutine


val double = coroutine { (x: Int) =>
  yieldval(x)↑
  yieldval(x)
}

val i = call(double(7))
var sum = 0
while (i.resume↑) { sum += i.value }

Calling a coroutine


val double = coroutine { (x: Int) =>
  yieldval(x)↑
  yieldval(x)
}

val i = call(double(7))
var sum = 0
while (i.resume) { sum += i.value↑ }

Calling a coroutine


val double = coroutine { (x: Int) =>
  yieldval(x)↑
  yieldval(x)
}

val i = call(double(7))
var sum = 0
while (i.resume↑) { sum += i.value }

Calling a coroutine


val double = coroutine { (x: Int) =>
  yieldval(x)
  yieldval(x)↑
}

val i = call(double(7))
var sum = 0
while (i.resume↑) { sum += i.value }

Calling a coroutine


val double = coroutine { (x: Int) =>
  yieldval(x)
  yieldval(x)↑
}

val i = call(double(7))
var sum = 0
while (i.resume) { sum += i.value↑ }

Calling a coroutine


val double = coroutine { (x: Int) =>
  yieldval(x)
  yieldval(x)↑
}

val i = call(double(7))
var sum = 0
while (i.resume↑) { sum += i.value }

Calling a coroutine


val double = coroutine { (x: Int) =>
  yieldval(x)
  yieldval(x)
}↑

val i = call(double(7))
var sum = 0
while (i.resume↑) { sum += i.value }

Calling a coroutine


val double = coroutine { (x: Int) =>
  yieldval(x)
  yieldval(x)
}↑

val i = call(double(7))
var sum = 0
while (i.resume) { sum += i.value }
↑

Coroutine instance operations

call - creates a coroutine instance
resume - resumes a coroutine instance
value - obtains the last yielded value
result - obtains the result of the invocation

Typing a coroutine


val double =
  coroutine { (x: Int) =>
    yieldval(x)
    yieldval(x)
  }

Typing a coroutine


val double: Int ~> (Int, Unit) =
  coroutine { (x: Int) =>
    yieldval(x)
    yieldval(x)
  }


val i: Int <~> Unit =
  call(double(7))

Coroutine composition

As coroutine definitions grow larger,
so does the need to decompose them into independent components.

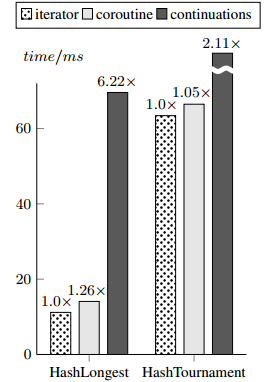
Example: hash table

A closed-addressing hash table is an array containing buckets.
A bucket is a list of elements.


  val array: Array[List[T]]

Example: hash table

Assume that we know how to traverse a list of elements.


val bucket =
  coroutine { (b: List[T]) =>

    var cur = b

    while (cur != Nil) {

      yieldval(cur.head)

      cur = cur.tail
    }
  }

Example: hash table

Then, we should be able to use that to traverse an array of lists.

val table =
  coroutine { (t: Array[List[T]]) =>

    var i = 0

    while (i < t.length) {

      bucket(t(i))

      i += 1
    }
  }

Coroutine composition

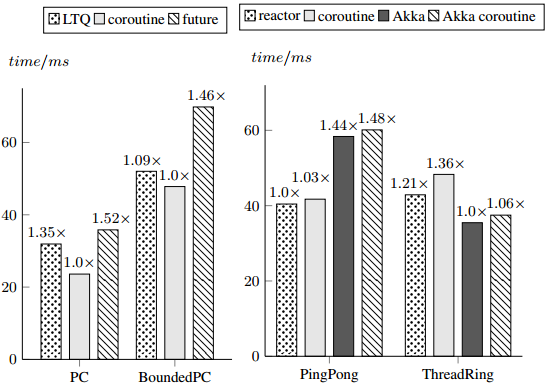
The direct call reuses the stack of the same coroutine instance.

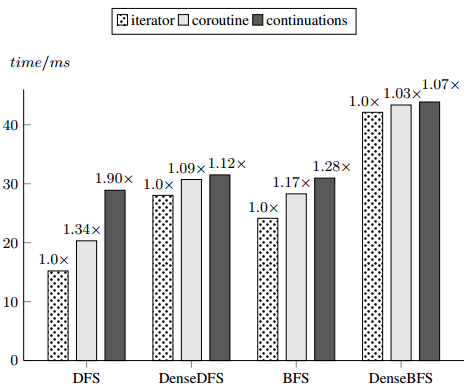
Use-cases

How do Scala coroutines generalize other models?

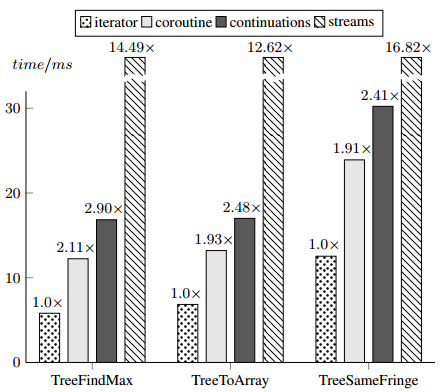
Iterators


def iterator(tree: Tree) =
  call(foreach(tree))


val it = tree.iterator
while (it.resume)
  println(it.value)

Iterators

Iterators follow directly from foreach definitions.


val foreach =
  (t: Tree[T], f: T => Unit) =>
    if (t != null) 
      foreach(t.left, f)
      f(t.elem)
      foreach(t.right, f)
    }

Iterators

Iterators follow directly from foreach definitions.


val foreach =
  coroutine { (t: Tree[T]) =>
    if (t != null) 
      foreach(t.left)
      yieldval(t.elem)
      foreach(t.right)
    }
  }

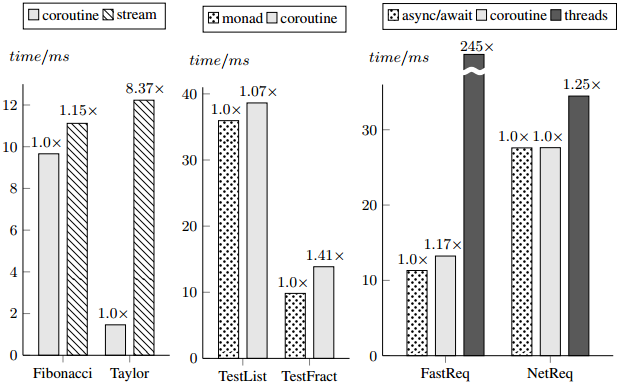
Async-Await

def loginRequest(): Future[String]
def httpRequest(c: String): Future[Page]

async {
  val credential =
    await { loginRequest() }
  val ui =
    await { httpRequest(credential) }
  ui.html
}

Async-Await

How do we define async and await using coroutines?

Async-Await

def await[R]: Future[R] ~> (Future[R], R) =

  coroutine { (f: Future[R]) =>

    yieldval(f)

    f.value.get.get
  }

Async-Await

def async[R](b: () ~> (Future[Any], R)) = {

  val i = call(b())

  val p = Promise[R]()

  @tailrec def loop(): Unit =
    if (i.resume)

      i.value.onSuccess(loop)

    else p.success(i.result)

  Future { loop() }
  p.future
}

Direct-Style Reactors

An actor must declare all receive operations
in terms of a top-level receive.


class Printer extends Actor {
  def receive = {
    case x: Int => println(x)
  }
}

Direct-Style Reactors

A reactor uses first-class events sources,
and receives by calling onEvent.


class Printer extends Reactor[Int] {
  main.events.onEvent { x =>
    println(x)
  }
}

Direct-Style Reactors

A reactor uses first-class events sources,
and receives by calling onEvent.


class Adder extends Reactor[Int] {
  operands.once.onEvent { x =>
    operands.once.onEvent { y =>
      println(x + y)
    }
  }
}

Direct-Style Reactors

This soon results in the pyramid of doom.
Instead, we want to write code without nesting.


class Adder extends Reactor[Int] {
  val x = operands.get()
  val y = operands.get()
  println(x + y)
}

Direct-Style Reactors

Challenge: implement methods react and get,
that define a reactor, and extract an event from its event source.

Direct-Style Reactors


type Obs = (() => Unit) => Unit


def get: () ~> (Obs, T) =

  coroutine { () =>
    var ret: T = _

    val obs = (cont: () => Unit) =>
      onEvent(x => { ret = x; cont() })

    yieldval(obs)

    ret
  }

Direct-Style Reactors


type Obs = (() => Unit) => Unit


def react[T](c: () ~> (Obs, Unit)) =

  Reactor[T] {
    val i = call(c())

    def loop() =
      if (i.resume) i.value(loop)

    loop()
  }

Simpler ScalaCheck tests

ScalaCheck tests typically used generators to explore the input space.


val tuples: Gen[(Int, Int)] =
  for {
    a <- choose(0, Int.MaxValue)
    b <- choose(0, a)
  } yield (a, b)


property("comm") = forAll(tuples) {
  a + b == b + a
}

Simpler ScalaCheck tests

More intuitive: backtracking without inversion of control.


property("comm") = {
  val a = choose(0 until Int.MaxValue)
  val b = choose(0 until a)
  a + b == b + a
}

Simpler ScalaCheck tests

type Program = Seq[() => Unit] <~> Unit


val choose:
  Seq[Int] ~> (Seq[() => Unit], Int) =

  coroutine { (vals: Seq[Int]) =>
    var res: Int = _
    yieldval(vals.map(x => () => res = x))

    res
  }

Simpler ScalaCheck tests

type Program = Seq[() => Unit] <~> Unit


val backtrack: Program ~> (Unit, Unit) =
  coroutine { (p: Program) =>

    if (p.resume) {

      for (prepare <- p.value) {
        prepare()

        backtrack(p.snapshot)
      }

    } else yieldval(())
  }

Simpler ScalaCheck tests


type Test = () ~> (Seq[() => Unit], Unit)


val forever =
  coroutine { (test: Test) =>
    while (true) {
      val p = call(test())
      backtrack(p)
    }
  }

Simpler ScalaCheck tests


def property(t: Test) = {
  val i = call(forever(t))
  for (i <- 0 until MAX_TESTS) i.resume
}


property {
  val a = choose(0 until Int.MaxValue)
  val b = choose(0 until Int.MaxValue)
  a + b == b + a
}

Equivalence with delimited continuations

type Shift = (() => Unit) => Unit

def reset(b: () ~> (Shift, Unit)) = {
  def continue(i: Shift <~> Unit) =
    if (i.resume)
      i.value(() => continue(i.snapshot))
  continue(call(b()))
}
def shift: Shift ~> (Shift, Unit) =
  coroutine { (b: Shift) =>
    yieldval(b)
  }

The most important type alias


type CoroutineAPI =

  CallbackStyleAPI => DirectStyleAPI


implicit val aBitOfWork =
  implicitly[TwentyLinesOfCode]

Thank you!

http://github.com/storm-enroute/coroutines